混合正态分布
的有关信息介绍如下: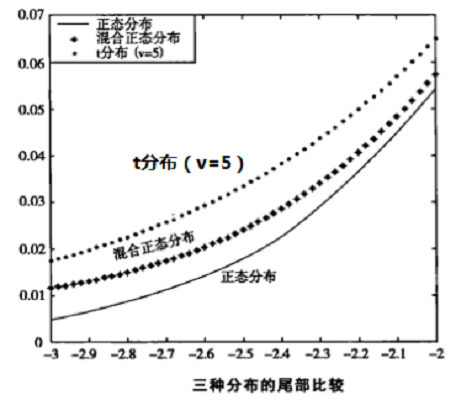
混合正态分布( mixture of normal distribution)具有厚尾。该模型认为对数收益率服从这样一个过程:dlogS(t)=μdt+σg(t)dW,μ和σ是单个交易的均值和方差,W是标准布朗运动。当g(t) 是常数时,此模型变成标准的几何布朗运动。 g(t) 是一个从属随机的过程,它刻画了市场的交易活动时间。如果g(t) 被假定为对数正态分布,该混合过程也被称为正态-对数正态混合。它的概率密度函数由Clark (1973)给出。
混合正态分布的关键是从属过程的概念。Clark(1973)假设交易量是价格波动的原因,以及交易量就是那个从属过程。假定个别交易是正态分布以及交易量是有限的,他证明混合正态分布具有厚尾。
混合正态分布直观的优势在于它直接与市场微观结构有关,如信息流、交易量和交易次数。在一般情况下,混合正态分布不服从时间缩放。一些混合正态分布可以描述波动集群。
想要了解更多“混合正态分布”的信息,请点击:混合正态分布百科



